ანტიქრისტე

იგორ სოლოვიოვი

არის თუ არა შტრიხ-კოდ EAN-13-ში რიცხვი 666?

საწყისი მასალები:

1) მღვდელმონაზონი ლუკა და ბერი პროდრომი, ათონის გრიგორიატის მონასტრიდან: "შტრიხკოდი და რიცხვი 666". გამოკვლევა მესამე (23.6.1997). ღირ. გრიგოლის სახელობის სავანე. 1997 წ. 23 ივნისი. გამოყენებულია ხსენებულ ნაშრომში დამოწმებული და აღწერილი შტრიხ-კოდ EAN-13-ის სკანერით დამუშავების მეთოდები.

2) სხვადასხვა დროს შტრიხ-კოდ სკანერებზე მომუშავე ორი დამოუკიდებელი ინჟინერ-პროგრამისტის ზეპირი გადმოცემა სკანერიდან კომპიუტერში კოდის გადაცემის მეთოდის შესახებ.

ტერმინოლოგია:

კოდი - შტრიხ-კოდი EAN-13.

შტრიხ-სიმბოლო - სხვადასხვა სისქის 2 შტრიხი, რომლის მეშვეობითაც გრაფიკულად წარმოსდგება ნებისმიერი ციფრი კოდში.

სასაზღვრე შტრიხები -  (Guard Bars, Guard Patterns) – წინ წამოწეული შტრიხული სიმბოლოები, რომლებიც მოცემულია კოდის ეტიკეტის დასაწყისში, შუაში და ბოლოში.

LGP - Left Guard Pattern – მარცხენა  სასაზღვრე შტრიხი.

CGP - Center Guard Pattern – ცენტრალური სასაზღვრე შტრიხი.

RGP - Right Guard Pattern – მარჯვენა სასაზღვრე შტრიხი.

სკანერი - შტრიხ-კოდის ეტიკეტიდან წამკითხველი და კომპიუტერში მისი გადამცემი მოწყობილობა (სალარო აპარატი ან ბანკომატი).

გამოკვლევის შედეგები:

ძირითადი წინაპირობა შეხედულებისა, რომ შტრიხ-კოდ EAN-13-ში (შემდგომში: კოდი) დაშიფრული რიცხვი, 666 არსებობს - ეს არის რიცხვ 6-ის გამოსახულების ვიზუალური მსგავსება ამ კოდის დამცავ (სასაზღვრო) შტრიხებთან. ამ მსგავსების შესამოწმებლად ერთმანეთს თეორიულად შეადარეს გრაფიკული და შინაგანი წარმოდგენები, ასევე სკანერის მიერ რიცხვ 6-ისა და კოდის სასაზღვრე შტრიხების დამუშავების მეთოდები.

1. შტრიხ-კოდ EAN-13-ის გრაფიკული წარმოდგენა.

1.1 რიცხვ 6-ისა და სასაზღვრე შტრიხთა გამოსახულების ზომები.

იმისათვის, რათა გრაფიკულად (შტრიხების სახით) წარმოვიდგინოთ ნებისმიერი რიცხვი კოდში, მათ შორის 6-იც, იყენებენ ვერტიკალური ზოლის შტრიხ-სიმბოლოს, რომელიც, თავის მხრივ, 7 კიდევ უფრო წვრილი ზოლისგან, ე. წ. მოდულებისგან შედგება, რომელთაგან თითოეული შეიძლება იყოს თეთრი ან შავი. სასაზღვრე შტრიხების წარმოდგენისთვის იყენებენ სხვადასხვა რაოდენობის მოდულებისგან შემდგარ მცირე ზოლებს.

LGP და RGP-სთვის იყენებენ ზოლებს 3 მოდულისგან.

CGP-სთვის კი ზოლს 5 მოდულისგან.

ქვემოთ მოტანილ ნახატზე გამოსახულია კოდის ეტიკეტი, სადაც განმარტებულია გამოყენებულ მოდულთა რიცხვი:

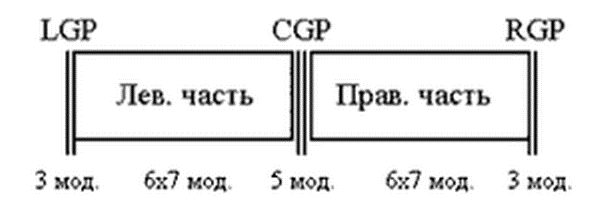
ნახ. 1. კოდის ეტიკეტი ერთ ნიშანზე გამოყენებული მოდულების რაოდენობის მითითებით

1.2 რიცხვ 6-ისა და სასაზღვრე შტრიხების გამოსახულება

კოდში გამოყენებული ნებისმიერი რიცხვის წარმოსადგენად გამოიყენება შტრიხ-სიმბოლოთა სამი სახე: Set A, Set B, Set C, ანუ ყოველი რიცხვი კოდის ეტიკეტზე წარმოდგენილია 3-დან ერთი რომელიმე ვარიანტით. ეტიკეტის მარჯვენა მხარეს განთავსებული რიცხვის გამოსახატავად ყოველთვის გამოიყენება Set C. მარცხენა მხარეს გამოიყენება Set A ან Set B № 1 ცხრილის შესაბამისად, და დამოკიდებულია შტრიხ კოდის პირველ  N რიცხვზე, რომელიც ეტიკეტზე LGP-დან მარცხნივ მდებარეობს.

ნახ. 2. კოდის ეტიკეტი (განმარტებით), რომელიც გამოიყენება მრავალ შტრიხში
ცხრილი 1. მამრავლები, რომლებიც გამოიყენება ეტიკეტის მარცხენა ნაწილში და კოდის რიცხვთა პროცენტული შეფარდებები, რომლებიც წარმოდგენლია Set A და Set B მამრავლებით:

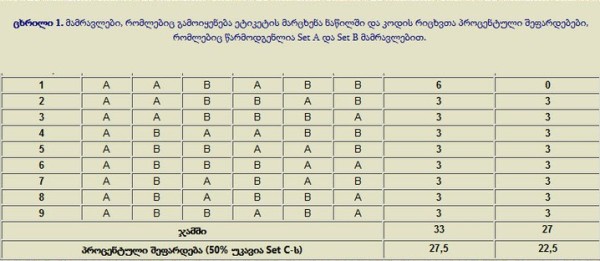
რიცხვი N ეტიკეტის მარცხენა მხარის ყოველი ციფრისთვის განსაზღვრავს რომელი მამრავლის (Set A თუ Set B) სიმბოლოთი იქნება წარმოდგენილი ეს ციფრი. მაგალითად, თუ ეტიკეტკის უკიდურეს მარცხენა პოზიციაში (ანუ LGP-დან მარცხნივ) დგას 2 (N=2), მაშინ 1 და 2-ე ციფრები წარმოდგენილნი არიან Set A-ს შტრიხ-სიმბოლოებით, 3-ე და 4-ე - Set B-თი, 5-ე - Set A-თი, ხოლო 6-ე Set B-თი.

ამგვარად, ნებისმიერი ციფრის, მათ შორის, ციფრ 6-ის, წარმოდგენის ყველა ვარიანტის დათვლის შემდეგ, ცხრილიდან ცხადი ხდება: კოდის ეტიკეტზე ციფრების ყველა შესაძლო შესატყვისობას (ანუ ეტიკეტების ყველა შესაძლო ვარიანტს) თუ ავიღებთ,  ყველა "ექვსიანის" 27,5% წარმოდგენილი იქნება Set A-ს შტრიხ-სიმბოლოების მამრავლებიდან, 22,5% Set B-დან და 50% - Set C-ს მამრავლებიდან.

რიცხვი 6 Set A,B და C-ს მამრავლებში და სასაზღვრე შტრიხები გამოისახებიან შემდეგი მეთოდებით:

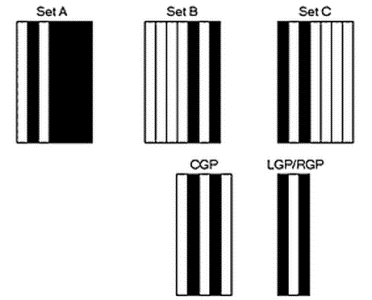
ნახ. 3. რიცხვ 6-ის გრაფიკული წარმოდგენა Set A-ში, Set B-ში, Set C-ში და კოდ EAN-13 სასაზღვრე შტრიხებში

ნახატიდან ცხადად ჩანს, რომ სასაზღვრე შტრიხების გამოსახულება ვიზუალურად ემთხვევა რიცხვ 6-ის გამოსახულებას მხოლოდ Set B-სა და Set C-ში, რაც შეადგენს 50%+22,5%=72,5 %, დანარჩენ 27,5%-ში (Set A) ეს გამოსახულებები ვიზუალურად ერთმანეთს არ ემთხვევა.


2. შიდა წარმოდგენა სკანერში

კოდის ეტიკეტის ნებისმიერ შტრიხ-სიმბოლოს სკანერი ორმაგ თანამიმდევრულ ნულებად და ერთიანებად (0 და 1) გარდაქმნის, სადაც ყოველ შავ მოდულს შეესაბამება 1, თეთრს კი - 0. მე-3 ნახატზე წარმოდგენილი სურათებთან შესაბამისად, გამოსახულებათა ორმაგი წარმოდგენები ღებულობენ ამგვარ სახეს:
6 (Set A) - 0101111;
6 (Set B) - 0000101;
6 (Set C) - 1010000;
LGP, RGP - 101;
CGP - 01010;.

ეს თანამიმდევრობანი არ შეიძლება განვიხილოთ როგორც ორობითი რიცხვი, არამედ როგორც ორმაგი გამოსახულებანი (სურათები რომლებიც შედგება 0-ებისა და 1-იანებისგან). სკანერის პროცესორის მეხსიერებაში ეს გამოსახულებანი წარმოდგენილია 8 თანრიგიანი ორმაგი სახით, მარცხნიდან ნულების დამატების გზით 8-ე თანრიგამდე. ამრიგად, ვღებულობთ:

6 (Set A) - 00101111;
6 (Set B) - 00000101;
6 (Set C) - 01010000;
LGP, RGP - 00000101;
CGP -      00001010;.

ცხადია, რომ ერთმანეთს ემთხვევიან მხოლოდ LGP/RGP-ს შიდა წარმოდგენათა და რიცხვ 6-ის (Set B) წარმოდგენის შიდა გამოსახულებანი, რაც შეადგენს კოდში მოცემული ყველა ექვსიანის 22,5% (იხ. § 1.2). LGP/RGP-ის შიდა წარმოდგენები არ ემთხვევიან CGP-ს შიდა წარმოდგენებს, ხოლო CGP-ს შიდა წარმოდგენა არ ემთხვევა რომელიმე 6-ანს.

სამწუხაროდ ამოსავალ მასალებში (1) მოცემული არ არის რიცხვ 6(Set C) -ის  8 თანრიგიანი წარმოდგენის მკაფიო აღწერა. წარმოდგენა 010100002 გამოყვანილია პროცესორსა და მეხსიერებაში ინფორმაციის წარდგენის საზოგადო წესების საფუძველზე. ამიტომაც, ის შესაძლოა იყოს არაზუსტი, თუკი სწორედ რიცხვ 6(Set C)-ისთვის სკანერის კონსტრუქციაში გაკეთებულია რაიმე გამონაკლისი, რაც პრაქტიკულად წარმოუდგენელია. ყოველ შემთხვევაში, ეს წარმოდგენა ადვილად შესამოწმებელია რომელიმე სხვა წყაროს დახმარებით.

3. სკანერის მიერ სიმბოლოს ამოცნობისა და დამუშავების ალგორითმი

საწყის მასალებში (1) დეტალურად არის აღწერილი "სიგანის მანძილის" (width distance) ტექნიკის ალგორითმი, რომელიც რიცხვ 6(Set B,C)-სა და LGP/RGP-ისთვის იძლევა ერთსა და იმავე შესატყვისობას: 3:2:1. მოცემული ალგორითმის თეორიული გამოყენება CGP-ს ამოსაცნობად შესაძლებლობას გვაძლევს დავასკვნათ:

CGP-სთვის შეიძლება მივიღოთ შესატყვისობა 4:3:2:1, რომელიც LGP/RGP-ს შესატყვისობისგან (3:2:1) განსხვავდება და გაშიფრვის დროს, ამ ალგორითმის აღწერის თანახმად, ორობითი სახით შემდეგ სურათს გვაძლევს:

00001111
-00000111
+00000011
-00000001

000010102 - ეს არის ზუსტად CGP-ს შიდა წარმოდგენა, რაც ადასტურებს 4:3:2:1 შესატყვისობის სინამდვილეს.

4. შტრიხ-სიმბოლოს, როგორც რიცხვ 6-ის იდენტიფიკაციის მომენტი

სკანერი თავისი მუშაობის შედეგებს გადასცემს კომპიუტერს, რომელთანაც ის კლავიატურის შესასვლელში კლავიატურასთან ერთად არის მიერთებული (იხ. სურ. 4) ერთ წერტილში (*). ასეთი მიერთება კეთდება ეტიკეტის კოდის ხელით შეყვანის შესაძლებლობის უზრუნველსაყოფად, უბრალოდ, კლავიატურიდან ციფრის აკრეფვის მეშვეობით. კლავიატურა კომპიუტერს გადასცემს აკრეფილი კლავიშების რიგით ნომრებს. რადგან სკანერი და კლავიატურა კომპიუტერთან ერთი საერთო წერტილით (*) არიან მიერთებულნი, სკანერი "იძულებულია" კომპიუტერს ასევე გადასცეს კლავიშების რიგითი ნომრები, რომლებიც უნდა აკრეფილიყო კლავიატურაზე, რათა ეკრანზე მივიღოთ ეტიკეტის შტრიხ-კოდის რიცხვთა თანამიმდევრობა.

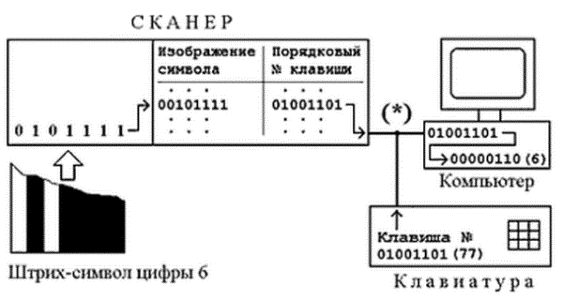
ნახ. 4. ინფორმაციის მარშრუტი ციფრ 6 (Set A)-ს შტრიხ-სიმბოლოდან კომპიუტერში 6-იანის ორმაგ წარმოდგენამდე.

ინფორმაციის მოძრაობა მიმდინარეობს შემდეგი სახით (4-ე ნახატზე ის ნაჩვენებია ციფრ 6(Set A)-ს შტრიხ-სიმბოლოს მაგალითზე). ეტიკეტის ნებისმიერ შტრიხ-სიმბოლოს სკანერი ნულებისა და ერთიანების (0 და 1) ორმაგ თანამიმდევრობად გარდააქცევს, რომელშიც ყოველ შავ მოდულს შეესაბამება 1, თეთრს კი - 0 (იხ. § 2). შემდეგ, ყველა ორმაგი თანამიმდევრობისთვის, რომლებიც კოდის ციფრებს შეესაბამებიან, განისაზღვრება კლავიატურის რიგითი ნომრები, რომლებიც აუცილებელი იქნებოდა ამ ციფრების ასაკრებად (ციფრ 6-იანისთვის კლავიშა # 77) და გადაეცემა კომპიუტერს. ამგვარად, სასაზღვრე შტრიხები კომპიუტერს არ გადაეცემა, ისინი იქ არც არიან საჭირონი ორი შემდეგი მიზეზის გამო:

1) სასაზღვრე შტრიხები თავის ფუნქციას გამოყონ ეტიკეტის კოდის მარჯვენა და მარცხენა ნაწილები ასრულებენ მხოლოდ მანამ, სანამ სკანერი გარდაქმნის მათ ორმაგ თანმიმდევრობად.

2) შტრიხ-კოდის ხელით შეყვანის შემთხვევაში კლავიატურაზე იკრიფება მხოლოდ ციფრის კოდი, შედეგად, კომპიუტერს გადაეცემა აკრეფილი ციფრული (0-9) კლავიშების რიგითი ნომრები ყოველგვარი სასაზღვრე შტრიხების გარეშე. რადგან სკანერი მიერთებულია კლავიატურის შესასვლეს ბუდეს, ის "იძულებულია" მხოლოდ ციფრული კლავიშების რიგითი ნომრებიც გადასცეს.

მხოლოდ კომპიუტერის შიგნით ხდება № კლავიშას ციფრად გარდაქმნა. ჩვენს შემთხვევაში, № მიხედვით, 77-ე კლავიშას აკრეფვისას კომპიუტერი განსაზღვრავს, რომ შეყვანილი იყო ციფრი 6.

ამგვარად, სკანერში არ არსებობს რიცხვ 6-ის რიცხობრივი წარმოდგენა (ორმაგი რიცხვი 00000110), არამედ არსებობს რიცხვ 6-ის გამოსახულების წარმოდგენა (იხ. § 2). რიცხვ 6-ის რიცხობრივი წარმოდგენა ჩნდება მხოლოდ კომპიუტერში, სადაც სასაზღვრე შტრიხები არანაირი სახით არ არსებობენ.

5. რიცხვ 6-ის შტრიხული გამოსხულებისა და სასაზღვრე შტრიხების მსგავსება

მოცემული პუნქტი, ინფორმაციის უკმარისობის გამო წარმოადგენს ვარაუდს, რომელიც იმდენად ლოგიკაზე არ არის დაფუძნებული, რამდენადაც საღ აზრზე.

5.1. ერთნაირი სიგანის ორი ზოლებისა და შუაში მოქცეული ერთი თეთრი ზოლის გამოყენება სასაზღვრე შტრიხებში.

ბერძენი ავტორების ნაშრომში ნათქვამია: "ეს შტრიხი ტექნიკურად მაკონტროლებლად უფრო გამოსადეგია კოდირების ამ ტიპში". ეს გამოსადეგობა კი იმაში გამოიხატება, რომ სკანერის მოწყობილობისთვის მოხერხებულია გამოსახულებების ერთეული, სერიული იმპულსების წაკითხვა:

ერთი შავი იმპულსი;
ერთი თეთრი იმპულსი;
ერთი შავი იმპულსი;

რომელიც იმპულსთა გრძლიობის ეტალონად იქნება გამოყენებული მომდევნო წაკითხვაში.

5.2 ერთი სიგანისა და ერთი თეთრშუალედიანი ორმაგი შტრიხების გამოყენება რიცხვ 6(Set B,C) გამოსახატავად.

რიცხვ 6(Set B,C)-ს გამოსახულება მიიღება ინვერტირების გზით (ყოველი შავი მოდული გადადის თეთრში და პირიქით) და რიცხვ 6(Set A)-ს საწყისი გამოსახულების შემდგომი სარკისებური გამოსახულებით. სავარაუდოდ, ჯერ შემუშავებული იყო რიცხვ 6(Set A)-ს გამოსაულება, ხოლო შემდეგ უკვე მისგან ავტომატურად იქნა მიღებული 6(Set B) და 6(Set C), რომლებიც შეესაბამებიან კიდევაც ორ თხელ ზოლს. სამწუხაროდ, ჯერ ვერ მოვიპოვეთ ინფორმაცია იმის შესახებ, თუ რამდენად აუცილებელი იყო რიცხვ 6(Set A)-ს საწყისი გამოსახვა სწორედ ამგვარი სახით.

დასკვნები:
იმისთვის, რათა გავაკეთოთ დასკვნა იმის შესახებ, რომ მათემატიკური თვალსაზრისით სასაზღვრე შტრიხები წარმოადგენენ სამ ექვსიანს (666), აუცილებელია ორი პირობის შესრულება:

ყველა სამი სასაზღვრე შტრიხი ერთმანეთს უნდა დაემთხვეს.

სასაზღვრე შტრიხების გამოსახულება უნდა დაემთხვეს რიცხვ 6-ის გამოსახულებას.

გამოკვლევიდან ცხადი ხდება, რომ ვიზუალური მსგავსების არსებობის შემთხვევაში, ადგილი აქვს მხოლოდ სასაზღვრე შტრიხების არაპირდაპირ დამთხვევას რადგან, შიდა წარმოდგენის დონეზე და ამოცნობის ალგორითმის შედეგთა გამოყენების დონეზე LGP/RGP შტრიხები არ ემთხვევიან ცენტრალურ შტრიხს CGP-ს.

ადგილი აქვს ასევე სასაზღვრე შტრიხებისა და ციფრ 6-ის არაპირდაპირ დამთხვევას, რადგან ციფრ 6-ის გამოსახულების სამი ვარიანტის არსებობის შემთხვევაში, სხვადასხვა Set A, Set B и Set C-ში, ციფრ 6-ის Set A-ში წარმოდგენა საერთოდ არ ემთხვევა სასაზღვრე შტრიხებს, Set C-ში ის არ ემთხვევა სკანერის შიდა წარმოდგენის დონეზე, და მხოლოდ Set B-ში (22,5% ციფრ 6-ის გამოსახვის ყველა შესაძლო ვარიანტიდან) ემთხვევიან სრულიად სასაზღვრე შტრიხები და ციფრ 6-ის გამოსახულებანი ერთმანეთს.

მოცემული გამოკვლევის წარმოებისას გამოიყენებოდა ინფორმაციის ანალიზის ცალმხრივი მიდგომა - წმიდად მათემატიკური. მაგრამ, ცნობილია, რომ რიცხვი 666, როგორც მხეცის რიცხვი - წმიდად სიმბოლური რიცხვია და მას, ამ მხრივ უკვე მათემატიკური მნიშვნელობა არ გააჩნია. შედეგად, ის სიმბოლურად უნდა იქნეს განხილული, რომელიც შედგება 6-იანის სიმბოლოსაგან. ექვსიანები, ამგვარად, კარგავენ თავიანთ მათემატიკურ მნიშვნელობას და ასევე ხდებიან სიმბოლონი. რაც რჩება რიცხვ 6-ის წარმოდგენის სამი ვარიანტიდან? - არაფერი, რადგან სიმბოლო შეიძლება ინვერტირებულ იქნეს (გარდაიქმნას ვერტიკალურად), შეიძლება სარკისებურად აისახოს (ჰორიზონტალურად) - და ის მაინც დარჩება 6-იანის სიმბოლოდ.

მსგავსი სიტუაციაა მარჯვენა მარცხენა (LGP/RGP) სასაზღვრე შტრიხებისა და ცენტრალური (CGP) შტრიხების განსხვავების შემთხვევაშიც. მარცხინდან (ან მარჯვნიდან) თეთრი ზოლების დამატება სიმბოლოს მნიშვნელობას არ ცვლის. ამგვარად, სასაზღვრე შტრიხები და ექვსიანები ერთმანეთს ემთხვევიან სიმბოლურად, შედეგად, კი შტრიხ-კოდი EAN-13 შეიცავს 666-ს.